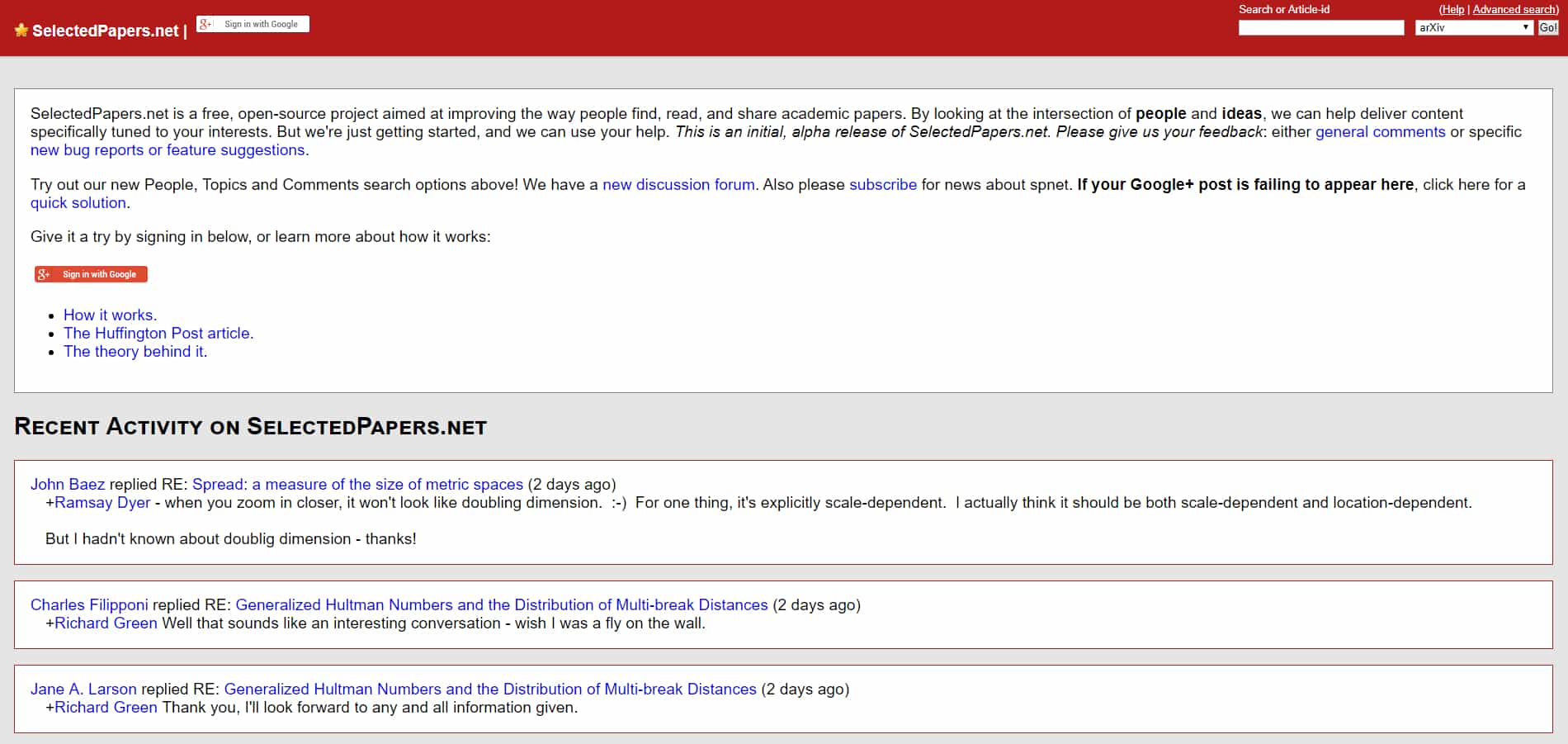
Selected Papers Network
The Selected Papers Network (also called SP Network) was an open-source project launched by Dr. Christopher Lee in 2013. It was created as a space where academics could read, share, and give feedback on articles and papers related to their field. The site allowed users to link their Google+ accounts so that their comments would be shared on social media as well as on the Selected Papers site. They had plans to support other social networks, like Twitter, but never got that far. They did create a system of tags to help facilitate conversation, like #mustread for a paper that a user thought was extremely important and #question for a post that was asking a question about a particular paper.
Open Peer Review
The entire system was based on the idea of open peer review. Typically, articles and papers are sent to academic journals, where they are reviewed by editors who decide whether or not they are fit to be published. There was a time when these journals were pretty much the only way to get access to scholarly papers, so they had tight control over what discoveries saw the light of day. But with the Internet, ideas can be directly shared with and reviewed by the larger public. The SP Network didn’t set out to replace journals, but they did aspire to work alongside them in the publishing process. A mathematician or scientist could post a paper to the site, gather comments and reviews from their peers, then ask the editor of a journal to consider this feedback when making their decision.


Dr. Christopher Lee
Born September 14th, 1966 in San Francisco, Dr. Christopher John Lee is a doctor of structural biology and a professor of Chemistry, Biochemistry, and Molecular Biology at UCLA. He has won several awards during his career, including the UCLA Seaborg Award and the American Cancer Society Postdoctoral Fellowship. His hope in creating the SP Network was to bring the research community together and tear down the boundaries between different fields, allowing for faster and more creative innovation.
The Problems With Traditional Publishing
Since their inception, journals have served as a form of peer review and publication. In recent years, however, they have also become an indicator of status that can make or break an academic’s career. This has led to many people withholding their research from the public until it has been published by a journal, which can be harmful, especially if the research pertains to medicine. And some of the bigger journals have built up sterling reputations that they don’t always live up to. Many will publish surprising, eye-catching studies, even if they are deeply flawed. A system that allows a network of peers to read and reflect on various studies would solve many of these problems.

The Use of Hashtags

Hashtags rose to prominence on Twitter and have since been co-opted by numerous other social networks. They allow users to easily search for the content they’re interested in. Academics have a number of hashtags they can use to find and communicate with their online peers. For example, #PhDchat connects people who are working on their postgraduate education. Researchers who need access to a particular paper can send out a distress call using #ICanHazPdf in the hopes that one of their followers can email them a copy of the study they need. And people can always use tags specific to their field (like #archaeology or #twitterstorians) to find tweets that are relevant to their work.
Academia in Social Media

While many view social media as nothing more than a distraction, it can serve as a useful tool if you know how to use it. Twitter is a great way to share findings with a wide audience, especially if there’s a prominent hashtag that people in your field follow. Students often use Facebook to create groups where they can discuss classes, collaborate on projects, and plan in-person study sessions. There are even a number of social media platforms that were built specifically for academia. ResearchGate gives researchers a place to upload journal articles, data, conference papers, posters, and code that aren’t archived elsewhere online. Academia.edu allows academics to upload papers, request feedback, and communicate with their peers.
Moving Forward
Technology has changed the way that people interact with each other, and that’s as true for scholars as it is for anyone else. While the SP network didn’t stand the test of time, the idea it was founded on is still alive and well. Millions of academics use social media to share their work, get feedback, and stay in touch with their peers. Some even use it to collaborate, making interdisciplinary research easier than ever. As time goes by, many social networks will rise and fall as the needs of the public shift. But whatever comes along next, academia will no doubt find a way to make use of its potential.

